It is important to know how these triangulations are generated. While not the only triangulation method, one method that is almost universally included is Delaunay triangulation. In this post, I explain what Delaunay triangulation is, why it is so popular, and the process that is followed by many programs.
What is a Delaunay triangulation?
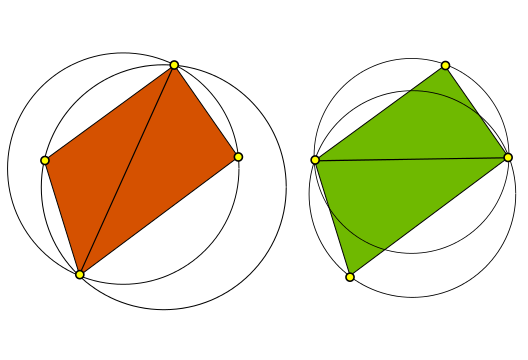
By definition, a Delaunay triangulation is a triangulation in which no vertex lies within the circumcircle of any triangle. The circumcircle of a triangle is simply the circle that passes through the three vertices of that triangle. Here is one very simple example. Each domain in the image below contains four points. There are exactly two triangulations for this domain. On the left, we see that one corner of each triangle is inside the circumcircle of the other. On the right, neither circumcircle encompasses the other triangle's opposing vertex. The case on the right is a Delaunay triangulation.Here you see the basic concept behind an implementation. First generate a triangulation, then check to see if any vertices fall within the cirumcircle of another triangle. If they do, simply swap the diagonal separating the two triangles. This will always give a Delaunay triangulation.
Why is it so popular?
Delaunay triangulation is fairly simple conceptually, but why is it so popular? The primary reason for its popularity is that the resulting mesh is inherently good quality. For a two-dimensional Delaunay triangulation, it can be shown that the minimum interior angle of each triangle is maximized, and that the maximum interior angle is minimized. The resulting triangles are as equiangular as possible. Another benefit is that the triangulation is independent of the order in which nodes are placed. It is also a relatively simple triangulation method to implement for convex hulls (think of a convex hull as a domain with no "dents" on the boundary). Implementation for non-convex hulls are a bit more challenging, but not impossible.The Process
The algorithm presented here is as described by S. W. Sloan in Ref. [1]. This routine generates a Delaunay triangulation for a set of predetermined coordinates.First, generate a triangle that encloses the entire domain to be triangulated. This triangle is called the supertriangle. The size and shape of the supertriangle is irrelevant, as long as all points in the domain are contained within.
The next portion of the algorithm is an iterative process. For each point in the domain, add the point to the triangulation by subdividing the triangle containing that point. You will then have a new node surrounded by three triangles, seen in green in the image below, and across the far edge of each new triangle is an opposing node, shown in red.
For each new triangle created, if the opposing node for that triangle is not part of the supertriangle, check whether the opposing node is within the circumcircle of the new triangle. If it is, swap the diagonal separating the newly inserted node and the opposing node. In the example, two diagonals need to be swapped.
Swapping the diagonal between two triangles gives two new triangles. Again, a circumcircle test is required for the new opposing nodes, and the process continues. until the circumcircle test is satisfied for all triangles connected to the recently inserted node.
The entire process then repeats until all nodes in the domain have been inserted and triangulated. The final step is to remove any triangles connected to the supertriangle vertices, leaving only the domain of interest. Below is a simple example to demonstrate the process one step at a time.
Extension into Three Dimensions
It is not difficult to see that Delaunay triangulation is possible in three dimensions. The obvious difference for a tetrahedral mesh is that a circumsphere is used instead of a circumcircle. One difference that is not so obvious is that instead of swapping the edge dividing two triangles, you need to swap a dividing face. However, when swapping a face, there are two alternative positions, so some care needs to be taken when choosing which option to use.Potential Uses
Delaunay triangulation, or any triangulation scheme for that matter, is great for connecting a known set of data points. I have used this in conjunction with barycentric interpolation to create a program that quickly interpolates to find values between known data points. It can also be used to generate a mesh for finite element and finite volume programs. Because the nodes can be inserted in an arbitrary order, it could even be used as a strategy to adapt a mesh in real-time.If this post was helpful, let me know in the comments. Ask questions if I have left something unclear, and I'll try to elaborate on the subject.
References
- S. W. Sloan, "A fast algorithm for constructing Delaunay triangulations in the plane", Adv. Eng. Software, Vol. 9, No. 1, pp. 34-55 1987



I'm a very rich and fancy rich person who buys all popular things. How much would you charge for a Delaunay triangulation? Do they come in three packs? Or is it a service? Can I be triangulated? Can my friends watch?
ReplyDelete-Guy Incognito
For a friend such as yourself, I would charge only slightly more than you are willing to pay. I suppose it would be a service, and I could do three just as easily as one. I could triangulate you if you gave me your coordinates. As for your friends watching, I think we'd just make fun of you. :)
DeleteAlways good to hear from you, friend.
And I from you, good buddy :)
Delete